우리가 다루는 로봇은 우리몸을 기계적인 음직임으로 ‘모델링’한 기계라고 생각하면 됩니다.  만화 영화에 나오는 로봇처럼 만들려면 아직도 한참 후의 이야기라고 생각하시면 됩니다. 그래도 그러한 복잡한 부분을 기계의 관절로 여겨서, 구분하여 연구하는 연구를 연구를 하시는 과학자들이 많이 있습니다.  이 분들의 연구를 운동학 분석(kinematic analysis)이라고 합니다.

참고

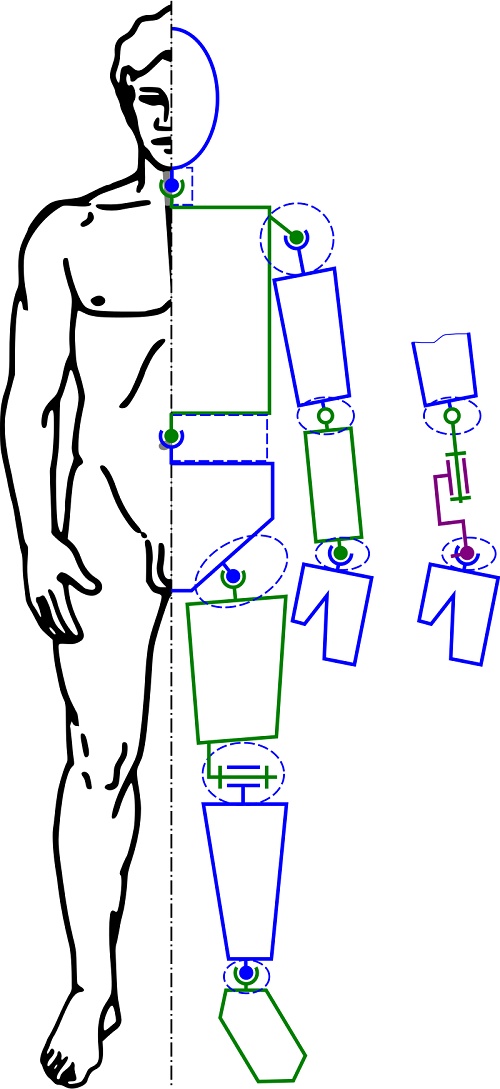
정방향 기구학에서 kinematics Equation Matrix 가구학은 각 로봇암의 관절의 회전 각도로 로봇암의 끝 (엔드이펙터: End effector라고 합니다.)의 위치를 x,y,z의 위치를 알아 내는것을 해 보았습니다. 우리는 이것을 관절의 좌표에서 직교좌표(cartesian coordinate)를 알아냈다라고 부릅니다. 증 입력은 각 관절의 각도이고 출력은 x,y,z 좌표인 수식이라고 생각하시면 됩니다.

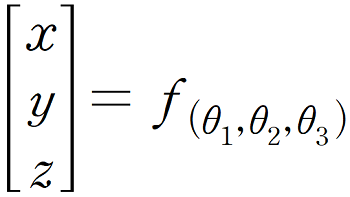
입니다.

이 처럼 x,y,x의 값으로 각 관절의 각도를 찾아내는 것을 역방향 기구학 (Inverse Kinematics)이러고 합니다. 보통 석박사들은 선형 대수학을 이용하여 설명하지만 이 이유는 것은 여러개의 CPU가 병력 처리로 고속으로 계산하는 컴퓨터를 사용한다는 생각에 그런 계산식으로 설명합니다. 우리는 간단한 MCU/CPU로 계산하므로 그런 선형 대수학 대신에 간단한 고등학교( 옆에 있는 한분은 이걸 초등학교때 배웠다고 합니다) 레벨의 기하학 수학으로 풀어 낼 수 있습니다.

삼각 함수중에 이러한 삼각형에 관한 수식이 있습니다.

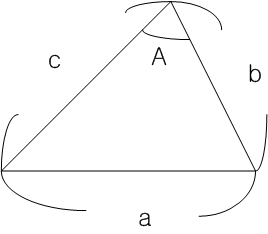
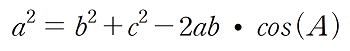
이것이 코사이 제 2 법칙이라는 공식인데 피타고라스의 법칙에서 조금 더 발전한 수식이라고 생각 하심 됩니다.   그러면 주어진 좌표가 있을 때 로봇 암의 각 각도를 찾아 보기로 합시다.

그 수식을 만들고 찾아내는 일은 제가 다 하였습니다.

이번에는 지난번 정방향 기구학의 x, y, z이 값으로 처음 주어 졌을때 그 각도가 나오는지 검증하면 정확한 계산이 되겠지요? 그러면 로봇 암의 각도를 기억하여 봅시다. 지난번 정방향 기구학 그림을 다시 불러 오겠습니다.

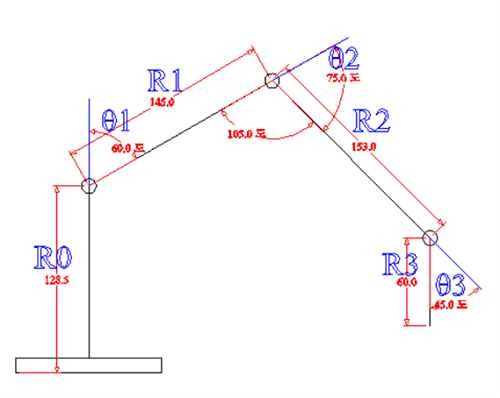
이때 각 관절의 길이와 x, y, z 좌표를 정리하여 봅니다.

 각 관절의 길이가 0 부터 

0번은, 1번은, 2번은, 3번은 

128.5mm, 145.0mm, 153.0mm, 60.90mm입니다. 

이때 주어진 각도에 end effector의 좌표가 x,y,z가 

x = 202.443mm, y = 116.881mm, z = -35.687mm

입니다.

각도를 계산하는 수식을 유도하는 것은 조금 머리를 쓰면 됩니다.

각 수식에서 필요한 중간 변수 RR, RT라는 변수를 채용하기로 합시다.

그 변수는

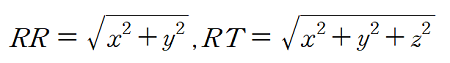입니다. 

이를 계산하면 RR = 233.761mm, RT = 236.47mm입니다.

아시는 분은 아시겠지만 ‘어 이거 피타고라스의 정리잖아!!“ 하실 분 많을 것입니다. 2500년전 수학자의 노고로 이렇게 로봇의 음직임을 계산할 수 있습니다. 이런 것을 피타고라스가 생각했을까요?

그러면 계산해 봅시다.

첫번째 관절 (로봇암의 회전각도를 정하는 수식)은

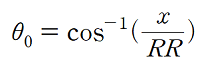
입니다.

sin, cos의 역 함수를 아크코사인이라고 하며 이 계산은 컴퓨터가 해 줍니다. 이 수식에 이렇게 값을 넣어주면 

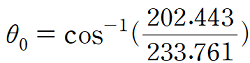
이고 각도가 30도가 계산됩니다.

우리의 로봇을 동작시키려면 괄호()안은 언제나 1보다 작아야 합니다. 

만일 1보다 크면 각도값이 허수값이 계산됩니다. 보통 고등학교 선생님들이 말씀하시는 '안된다'가 아닙니다.  이것은 다른 레벨의 이야기이고 상상속의 삼각함수가 존재하는 좌표계라고 생각 하시면 됩니다. (헬박사의 조언: 수학은 안 된다가 아니라 더 큰 세상이 있다.)

다음 계산하기 쉬운것 부터 계산하도록 합시다.

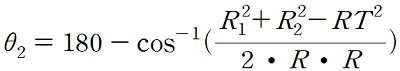
값으로 계산하면 75도가 나옮니다.

다음 남은것은 θ1입니다. 이것을 계산하기 위한 중간 변수로 중간 변수 두개를 채용하기로 합시다

첫번째는 

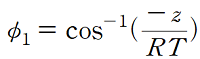
로 값은 81.32도가 계산됩니다.

두 번째는

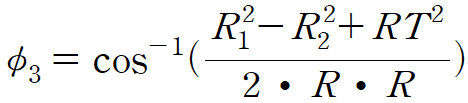
입니다. 이 계산값은 38.68도

이를 이용하여 θ1을 구하면 됩니다. 

θ1 = 180-Ø1-Ø3

위에서 계산한 값을 넣으면 

​ 

θ1 = 180-81.32-38.68

헉 60도가 계산됩니다.

그림을 보시면 x, y, z의 계산이 맞지요?

이럴 수가~~~

캬~~~

그럼 다음은 로봇 차렷 자세 만들기